Introduccion:

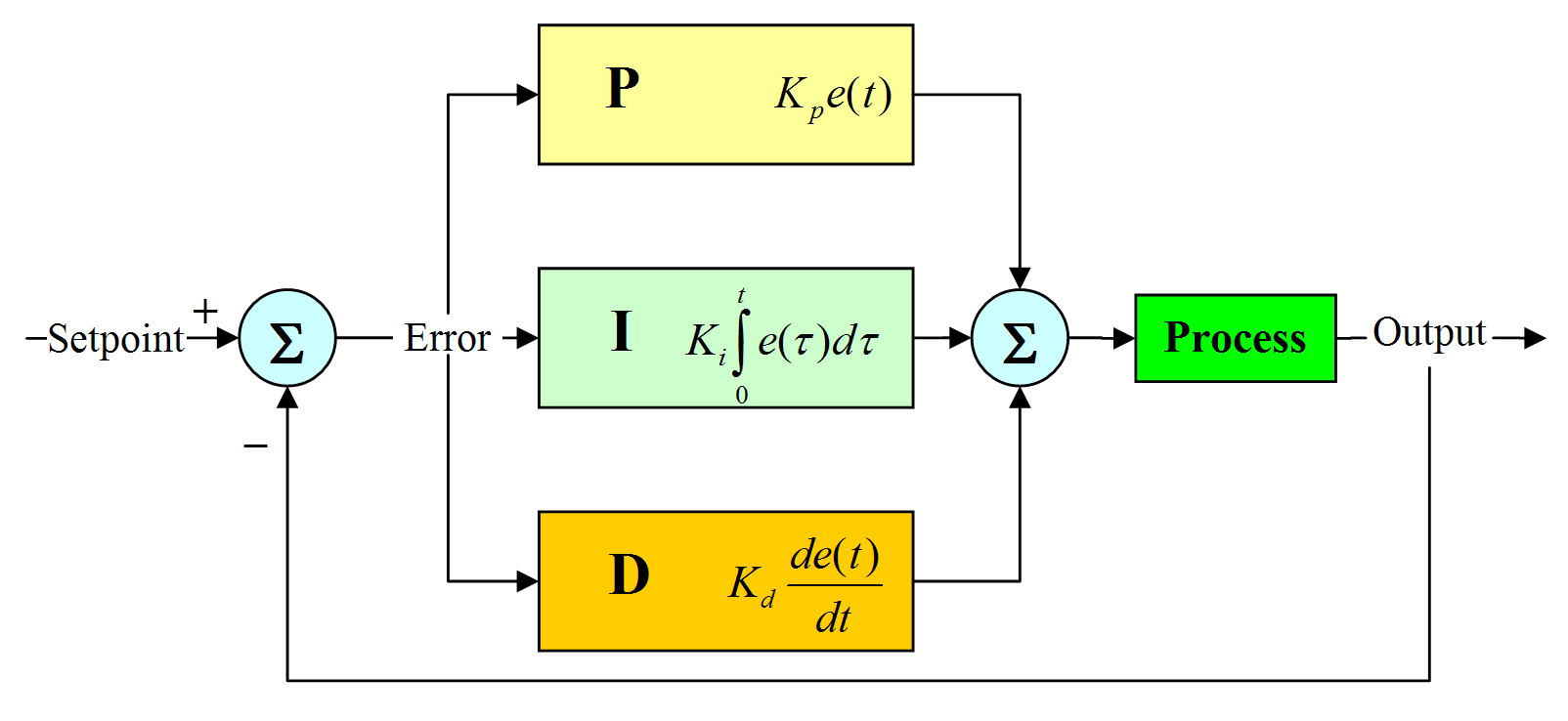
En este blog aprenderemos las características de los controles P (Proporcional), I (Integral) y D (Derivativo), para poder utilizarlos y obtener una respuesta de nuestro sistemas. Aqui podemos apreciar la representacion de un sistemas con retroalimentacón unitaria

 

En el grafico podemos ver la planta a controlar y el controlador que nos ayuda a ver el comportamineto de la planta.

La sintonización de los controladores Propor-cional - Integral - Derivativo o simplemente controladores PID, consiste en la determinación del ajuste de sus parámetros (Kc, Ti, Td), para lograr un comportamiento del sistema de control aceptable y robusto de conformidad con algún criterio de desempeño establecido.

Para poder realizar la sintonización de los controladores, primero debe identificarse la dinámica del proceso, y a partir de ésta determinar los parámetros del controlador utilizando el método de sintonización seleccionado.  

Hay que establecer los diferentes tipos de funcionamiento que pueden presentarse en un lazo de control realimentado, en el cual  hay dos entradas el valor deseado r(t) y la perturbación z(t) y una salida la señal realimentada y(t)

 

 Considerando las variables en el dominio de la variable compleja s y se define Gc(s) y Gp(s) como la función de tranferencia del controlador y de la planta respectivamente, a partir del diagrama del bloques del sistema de control de lazo cerrado, se obtiene que la señal realimentada, representación de la variable controlada, está dada por:

 

Aqui debemos tener en cuenta que hay dos posibles condiciones de operación del sistema de control en primer lugar.

Servomecanismo (z = 0)

   

Estorequiere de un seguimiento para el valor deseado, en segundo lugar:

Regulador (r=0)

 

Dado que los numeradores de las funciones de transferencia de lazo cerrado (2) y (3) son diferentes, no necesariamente un buen ajuste del controlador para operar como servomecanismo, proveerá un buen funcionamiento como regulador, razón por la cual se han desarrollado procedimientos de sintonización para ambos tipos de operación.

En la industria de procesos, la mayor parte de los controladores se utilizan para responder a un cambio en la perturbación, y se requiere de una buena regulación para seguir el cambio en el valor deseado, con excepción de los controladores esclavos en los sistemas de control en cascada.

Si el controlador se ha sintonizado para lograr una buena respuesta en un cambio en el valor deseado, no eliminará las perturbaciones en forma efectiva, si el sistema contiene un integrador o si su constante de tiempo es grande.

Es importante, entonces, determinar los requisitos de funcionamiento del lazo de control para seleccionar el procedimiento de sintonización adecuado.

El desarrollo de los métodos de sintonización ha sido extenso desde que Ziegler y Nichols propu- sieron su procedimiento en 1942. Normalmente, se dividen en métodos de lazo abierto y métodos de lazo cerrado.

Método de Lazo Abierto

Es el camino mas corto entre la entrada y la salida de un sitema.

Produciendo un cambio escalón a la salida del controlador se obtiene la curva de reacción del proceso.

Método de Lazo Cerrado

El controlador opera automaticamente produceiendo un cambio en el valor deseado se obtiene información del comportamineto dinámico del sitema para identificar un modelo de orden reducido para el proceso, o de las características de la oscilación sostenida del mismo, para utulizarla en el càlculo de los parámetros del controlador.

Controladores

Los controladores PID tienen algunas de las sigueinetes funciones de tranferencia.

Controlador PID-Ideal

 

Controlador PID-Serie 

 

Controlador PID-Industrial 

  

 

  

Metodo de Sintonización de Lazo Abierto

Los procedimientos de sintonización de lazo abierto utilizando un modelo de la planta que se obtiene, a partir de la curva de reacción del proceso, tenemos los siguientes:

MODELOS

  

A continuaciòn presenta algunas de las técnicas de identificación de lazo abierto y lazo cerrado más utilizadas para la obtención de estos modelos.

Método de Ziegler y Nichols

El criterio de desempeño que seleccionaron fue el de un decaimiento de 1/4, o sea que el error decae en la cuarta parte de un periodo de oscilación.

Las  ecuaciones fueron  determinadas  de  forma empírica a partir de pruebas realizadas en el laboratorio con diferentes procesos,  y están basadas en un modelo de primer orden más tiempo muerto identificado por el método de la tangente, para un funcionamiento del lazo de control como regulador con un controlador PID-Ideal.

 

Para poder determinar la respuesta al escalón de la planta o sistema controlado, se debe retirar el controlador PID y sustituirlo por una señal escalón aplicada al accionador.

 

En la siguiente figura se muestra la modificación que hay que realizar al sistema de control en lazo cerrado para convertirlo en un sistema en lazo abierto que responda a una señal escalón, retirando el controlador PID:

 

 

En la imagen siguiente se puede ver representado en rojo la entrada escalón al accionador o señal c(t). En azul se representa la salida del sistema medida por el sensor o señal h(t). El escalón de entrada c(t) debe estar entre el 10% y el 20% del valor nominal de entrada.
Como puede apreciarse, la respuesta del sistema presenta un retardo, también llamado tiempo muerto, representado por T1.

Para calcular los parámetros se comienza por trazar una línea recta tangente a la señal de salida del sistema (curva azul). Esta tangente está dibujada en la imagen con una recta a trazos.
El tiempo T1 corresponde al tiempo muerto. Este es el tiempo que tarda el sistema en comenzar a responder. Este intervalo se mide desde que la señal escalón sube, hasta el punto de corte de la recta tangente con el valor inicial del sistema, que en este caso es el valor 25ºC
El tiempo T2 es el tiempo de subida. Este tiempo se calcula desde el punto en el que la recta tangente corta al valor inicial del sistema hasta el punto en el que la recta tangente llega al valor final del sistema.

 

Además de estos dos tiempos característicos también hay que calcular la variación de la señal escalón dX y la variación de la respuesta del sistema dY.
En el caso de ejemplo que aparece en las imágenes, la variación de la señal escalón corresponde a dX = 5 voltios de señal de control c(t) y la variación del sistema corresponde a dY = 200ºC medidos por el sensor h(t).
A partir de estos valores se puede calcular la constante del sistema Ko:

Ko = (dX * T2) / (dY * T1)

Y a partir de la constante Ko se pueden calcular los parámetros del controlador PID con acción solo proporcional (P), proporcional e integral (PI) o proporcional integral y derivativa (PID):

 

La constante Kp corresponde a la ganancia proporcional, Ti es la constante de tiempo integral y Td es la constante de tiempo derivativa. En el caso de tener el controlador PID configurado con las ganancias integral Ki y derivativa Kd en vez de los tiempos Ti y Td, hay que tener en cuenta las siguientes relaciones entre ellos:

Ki = Kp / Ti
Kd = Kp * Td

Con lo cual la tabla de valores para ajustar el controlador PID será la siguiente:

 

Método de Cohen y Coon

En el desarrollo de su método de sintonización Ziegler y Nichols no consideraron que el proceso fuera auto regulado.  Cohen y Coon[8]   introduje- ron,  entonces,  un índice de auto regulación de- finido como m = tm/t y plantearon nuevas ecua- ciones de sintonización.  Estas se basan en el me- jor modelo de primer  orden más tiempo muerto que se pueda obtener   para lazos de control que funcionan como regulador, con el criterio de de- sempeño de decaimiento de 1/4 con sobrepaso mí- nimo, y con mínima área bajo la curva de respues- ta, y  un  controlador PID-Ideal.   Las ecuaciones son:

Método de López, Miller, Smith y Murril

El primer método basado en criterios integrales que presentó ecuaciones para el cálculo de los parámetros del controlador fue desarrollado por López et aly es conocido  como el método de López.

Definiendo una función de costo de la forma:

Donde F es una función del error y del tiempo,se obtiene un valor que caracteriza la respuesta del sistema.   Entre menor sea el valor de F, mejor será el desempeño del sistema de con- trol,  por ello, un desempeño óptimo se obtiene cuando F es mínimo.

Como F es una función de los parámetros del controlador (Kc, Ti, Td ), el valor mínimo de F se obtiene resolviendo las siguientes ecuaciones:

La optimización de los criterios de desempeño in- tegrales de López está basada en el mejor modelo de primer orden más tiempo muerto que se pueda obtener, para lazos de control que funcionan como reguladores con un controlador PID-Ideal.

Las ecuaciones de sintonización son:

Método de Kaya y Sheib

Mientras López desarrolló el método de sintonización  para  un  controlador  PID-Ideal,  Kaya  y Sheib   realizaron lo  mismo para controladores que denominaron PID-Clásico (PID-Serie), PID- No Interactuante (una variación del PID-Paralelo) y PID-Industrial.

El procedimiento de sintonización está basado en el mejor modelo de primer orden más tiempo muerto que se pueda obtener para lazos de con- trol que funcionan como reguladores. El criterio de desempeño corresponde a la minimización de alguno de los criterios integrales y el controlador a uno de los indicados anteriormente.

Las ecuaciones de sintonización son las mismas dadas por López (14) y los valores de los parámetros a a f se muestran en el Cuadro

Método de Sung, O, Lee, Lee y Yi

Los métodos de sintonización de controladores que optimizan los criterios integrales, vistos anteriormente, se basan en un modelo de primer orden más tiempo muerto. Sung et al. Por su par- te, basó su procedimiento de sintonización en un modelo de segundo orden más tiempo  muerto para un proceso como el dado por (9b), identificado mediante la realización de una prueba con realimentación por relé, seguida por una con control P.

El procedimiento está basado en el mejor modelo de segundo orden más tiempo muerto que se pueda obtener para lazos de control que funcionan como reguladores. El criterio de desempeño corresponde a la minimización de la ITAE y el controlador un PID-Ideal.  El ajuste de las ecuaciones la realizaron para 0,05 £ tm/t £ 2,0.

Las ecuaciones de sintonización son:

MÉTODOS DE SINTONIZACIÓN DE LAZO 

CERRADO

Este método no requiere retirar el controlador PID del lazo cerrado. En este caso sólo hay que reducir al mínimo la acción derivativa y la acción integral del regulador PID. El ensayo en lazo cerrado consiste en aumentar poco a poco la ganancia proporcional hasta que el sistema oscile de forma mantenida ante cualquier perturbación. Esta oscilación debe ser lineal, sin saturaciones. En este momento hay que medir la ganancia proporcional, llamada ganancia crítica o Kc, y el periodo de oscilación Tc en segundos.

Una vez hallados estos dos parámetros se pueden calcular los parámetros del controlador PID con acción solo proporcional (P), proporcional e integral (PI) o proporcional integral y derivativa (PID):

Ejemplo de sintonización de PID con la ganancia crítica

Vamos a realizar una sintonización del sistema térmico simulado anteriormente:

Control de temperatura

La primera operación será la de anular las acciones derivativa e integral:

Kd = 0

Ki = 0

Si el sistema PID utilizase tiempos, habría que hacer Td = 0 y Ti = infinito

A continuación se fija una temperatura de trabajo en la referencia y se aumenta la ganancia proporcional hasta conseguir una respuesta oscilatoria mantenida.

Con una ganancia proporcional Kp = 0.40 la respuesta todavía está amortiguada:

Al aumentar la ganancia proporcional hasta Kp = 0.43 se obtiene una respuesta con oscilaciones mantenidas:

Al aumentar la ganancia hasta Kp = 0.45, las oscilaciones crecen en el tiempo.

En este caso, por lo tanto, la ganancia crítica y el periodo son:

Kc = 0.43

Tc  = 21/4 = 5.3

A partir de este valor se calculan los parámetros del controlador PID:

Como puede comprobarse, los valores son semejantes a los valores obtenidos anteriormente con el método de la respuesta al escalón.

Introduciendo estos valores en la hoja de cálculo se obtiene la siguiente respuesta del sistema térmico con controlador PID:

En este caso también se puede terminar de afinar el regulador PID a mano para conseguir una respuesta un poco más rápida y estable.

Referencias:

Método de sintonización PID

Metodo ziegler-nichols

Control PID Clásico

Método de Sintonización de Controladores PID que operan como Reguladores

Trabajo realizado por:

Ney Andrade, Adriana Naranjo, Rolando Tipan y Lino Freire, estudiantes de la ESPOCH ING. CONTROL Y REDES INDUSTRIALES